General procedure to find centroid of composite areas, Solved Example Problems
Composite areas can be divided into several basic areas for which the location of centroid is known.
Centroid of Composite Areas
Composite areas can be divided into several basic areas for which the location of centroid is known.
• These basic areas and the location of their centroids are summarized in Table 5.3.1.
• Each basic area is considered to be concentrated at its centroid. Replacing integration by summation in formulae for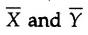 of centroid,
of centroid,

General procedure to find centroid of composite areas
1) Choose an appropriate origin and a co-ordinate system.
2) Divide the body into basic shapes illustrated in Table 5.3.1. If any of the basic shape has to be removed, treat its area to be negative.
3) Locate the centroid of each basic shape as illustrated in Table 5.3.1.
4) Write the co-ordinates of centroids of basic shapes with respect to the chosen origin as (x1, y1), (x2, y2) etc.
5) Use formulae to find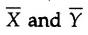 .
.
Note If any horizontal or vertical line of symmetry can be easily obtained, centroid will lie on that line. This can be used to determine either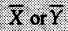 directly without any calculations.
directly without any calculations.
6) When objects are suspended from some point, the centroid lies on the vertical line passing through the point of suspension. If the point of suspension is chosen as origin, the centroid lies on Y-axis for which![]() = 0.
= 0.
For plane lamina,
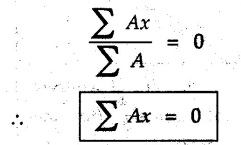
Such problems can also be solved by taking moment of area about the point of suspension. The total moment about the point of suspension will be zero for equilibrium, considering moments due to areas on left side of the point of suspension as positive and those on right side as negative. (The sign convention can be taken opposite to this).
7) In problems of finding some length when location of centroid is given, take moment about an axis passing through the centroid. The total moment of all the areas will be zero. For moment about vertical axis, choose sign convention as in suspended objects. For moment about a horizontal axis, we can consider the moment due to area above the axis as positive and below the axis as negative.
8) To find angle made by any line on an object with the horizontal or vertical when it is suspended from any point on it, locate the centroid co-ordinates with respect to the point of suspension. Find the angle @ made by the line joining the point of suspension to the centroid with vertical. When freely suspended, this line will rotate through angle @ and become vertical. Every line on the object will rotate through the same angle from its original position. This can be used to find the angle made by any line on the object with the horizontal or vertical.
These concepts are illustrated in the following examples.
Solved Examples for Understanding
Example 5.3.1
Locate the centroid of the area shown in Fig. 5.3.1. The dimensions are in mm.
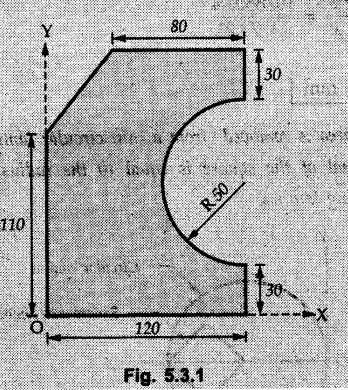
Solution:
The given area can be obtained by subtracting triangle and semicircle from rectangle as shown in Fig. 5.3.1 (a).
The calculations are tabulated as follows:

Example 5.3.2
A square area is removed from a thin circular lamina of radius r as shown in Fig. 5.3.2. The diagonal of the square is equal to the radius of the circle. Locate the centroid of the remaining lamina.
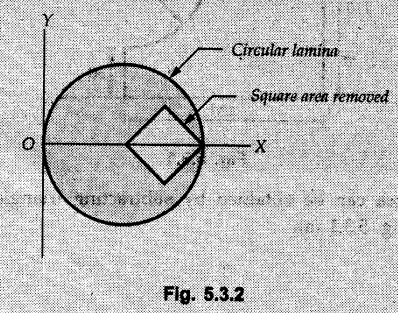
Solution:
Due to symmetry,![]() = 0
= 0
For the circle,
Α1 = πr2
Centroid of the circle is at its centre.
⸫ x1 = r
Length of diagonal of square = r
⸫ Length of each side = r/√2
For square,
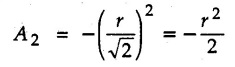
Centroid of square is at the centre of its diagonal.
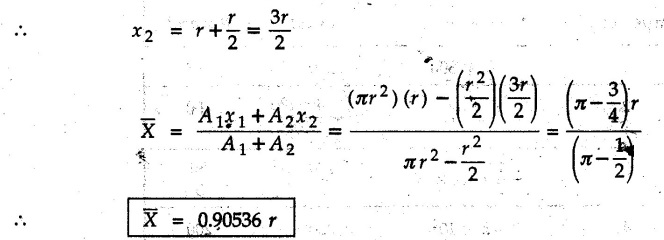
Example 5.3.3
Locate the centroid of the plane area shown in Fig. 5.3.3.
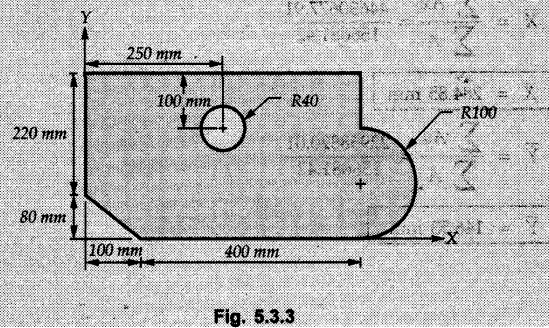
Solution:
Divide the given area as shown in Fig. 5.3.3 (a).
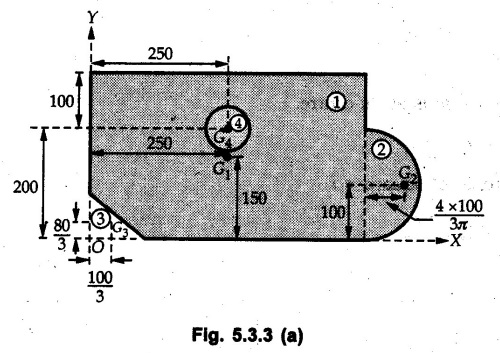
The calculations are tabulated as follows:

Example 5.3.4
Determine the centroid of the unsymmetrical I-section shown in Fig. 5.3.4
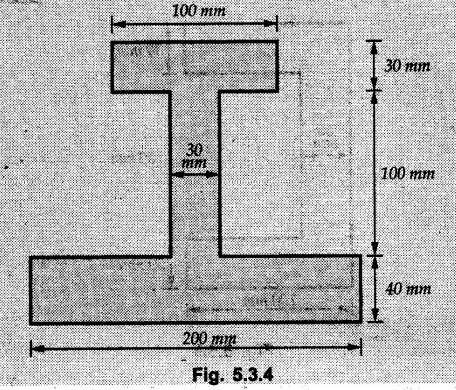
Solution :
Take co-ordinate axes and origin as shown in Fig. 5.3.4 (a) and divide the given section into three rectangles.
The given section is symmetric about a vertical line passing through the centre.

Example 5.3.5
Determine the centroid of the channel section shown in Fig. 5.3.5
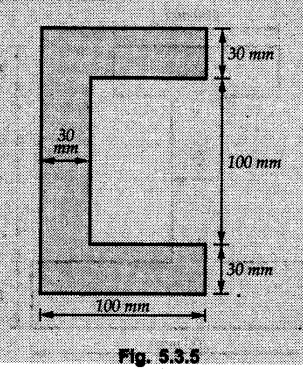
Solution:
The given section is symmetric about a horizontal line passing through the centre.
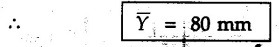
To find![]() take the leftmost vertical line to be reference and divide the area into three rectangles as shown in Fig. 5.3.5 (a).
take the leftmost vertical line to be reference and divide the area into three rectangles as shown in Fig. 5.3.5 (a).
Example 5.3.6
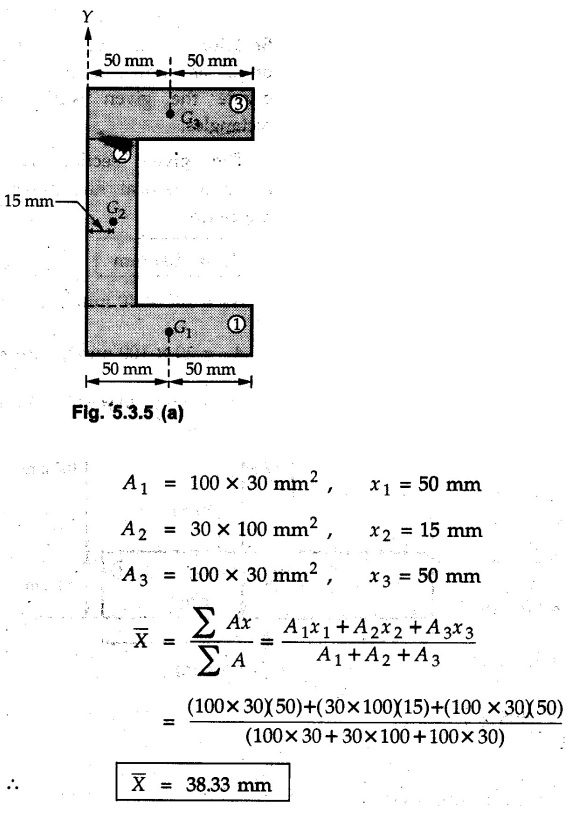
Find the centre of gravity of the L-section shown in Fig. 5.3.6.
Solution:
Take G as the origin and divide the L section into two rectangles GDEF and ABCD.
For rectangle GDEF,
A1 = 8 × 2 = 16 cm2
x1 = 4 cm, y1 = 1 cm
For rectangle ABCD,
A2 = 10 × 2 = 20 cm2
x2 = 1 cm, y2 = 2 + 5 = 7 cm

Example 5.3.7
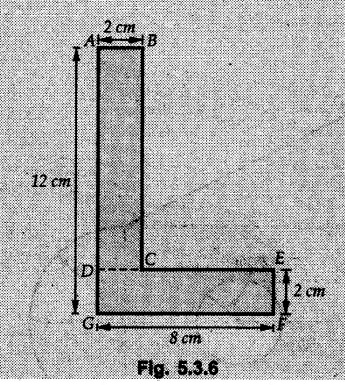
Determine the position of centroid for the lamina with a circular cutout shown in Fig. 5.3.7
Solution:
Divide the given area into a triangle, a rectangle and a semicircle from which a circle is removed as shown in Fig. 5.3.7 (a).
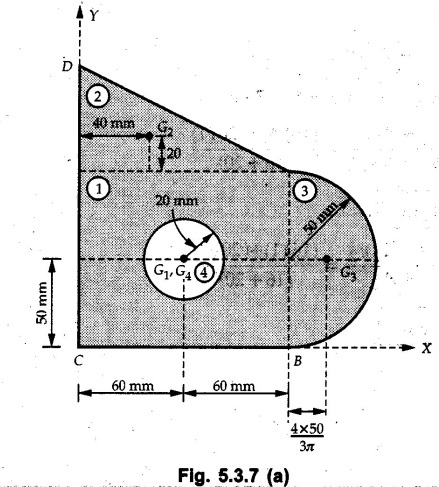
The calculations are tabulated as follows:
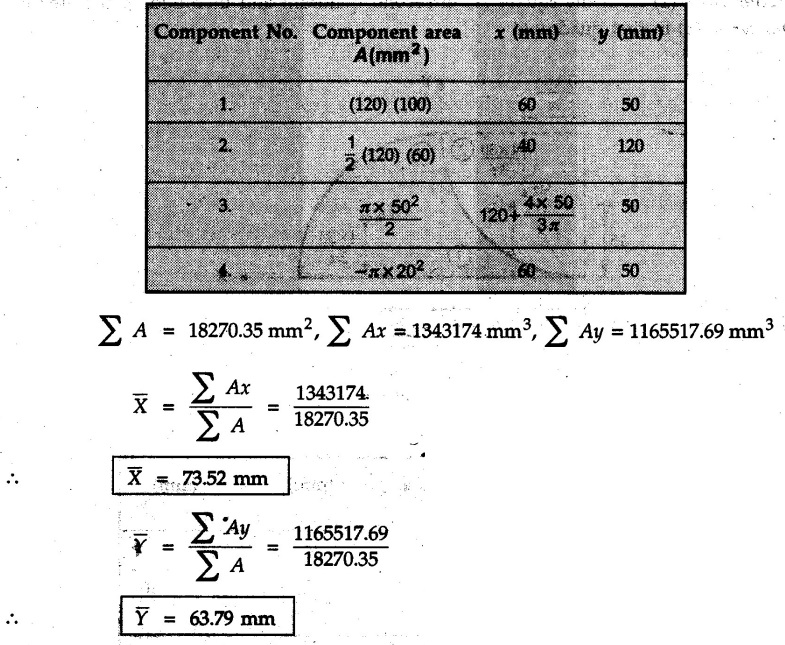
Example 5.3.8
Locate the centroids of the following area. Refer Fig. 5.3.8.
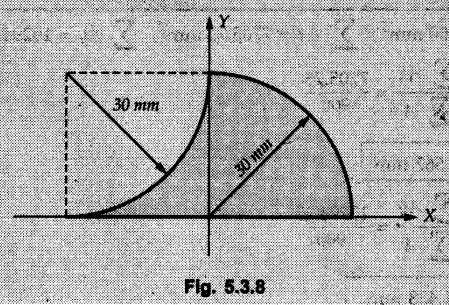
Solution:
The shaded portion in the Fig. 5.3.8 can be obtained by subtracting the area of quarter circle (2) from the square (1) in second quadrant and then adding the area of quarter circle (3) in first quadrant.
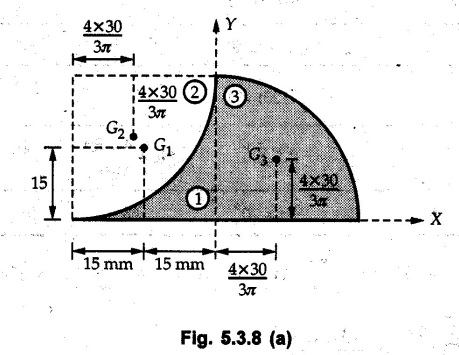
The calculations are tabulated as follows:

Example 5.3.9
Determine centroid of the shaded area with reference apex.
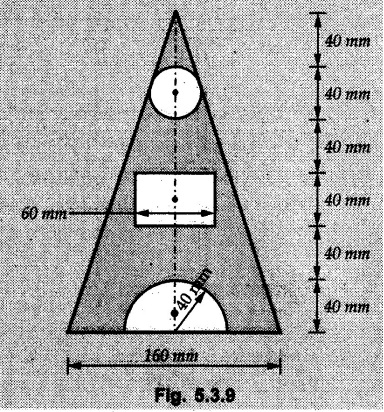
Solution:
The shaded area can be obtained by removing the circle, rectangle and semi-circle from the triangle. As the area is symmetric about a vertical line passing through the centre, centroid lies on this line, of symmetry. We take base of the triangle as reference for writing Y-co-ordinates of centroid.

The distance from apex = 240 – 82.02 = 157.98 mm
Example 5.3.10
Determine the position of centroid with respect to ‘O’
Solution:
As the given area is symmetric about a vertical line passing through the centre,
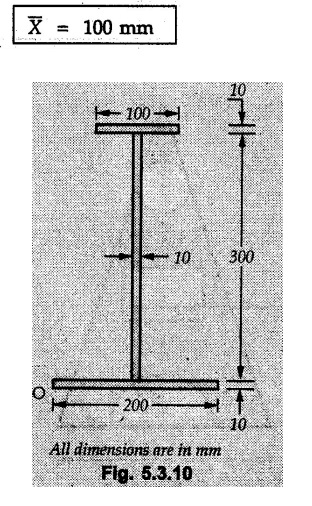
The given area can be divided into three rectangles.
A1 = 200 × 10 mm2 ; y1 = 5 mm
A2 = 10 × 300 mm2; y2 = 160 mm
A3 = 100 × 10 mm2; y3 = 315 mm
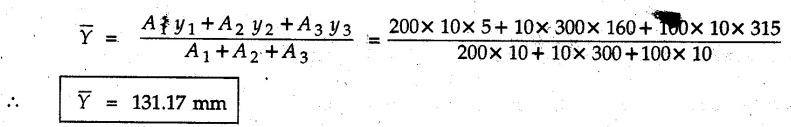
Example 5.3.11
Determine the position of the centroid for the shaded area with respect to the axes as shown in Fig. 5.3.11.
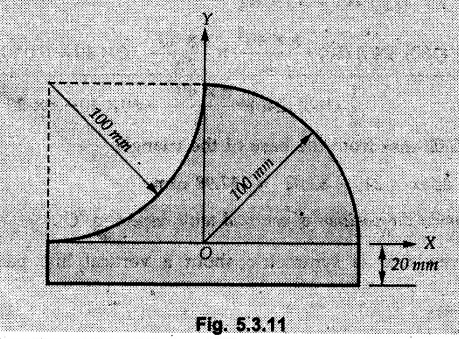
Solution:
The shaded region can be obtained by adding areas of square, rectangle, quarter circle and then subtracting a quarter circle as shown in Fig. 5.3.11 (a).
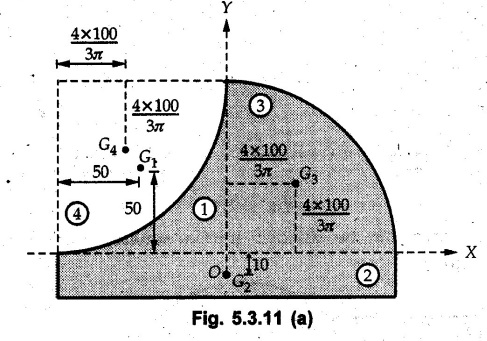
The calculations are tabulated as follows:

Example 5.3.12
Find the co-ordinates of centroid of the lamina, shown in Fig. 5.3.12 with Fig. 5.312 with respect to point A.
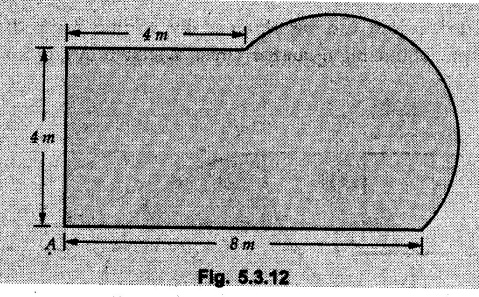
Solution:
The given area can be divided into a square, triangle and semi-circle as shown in Fig. 5.3.12 (a).
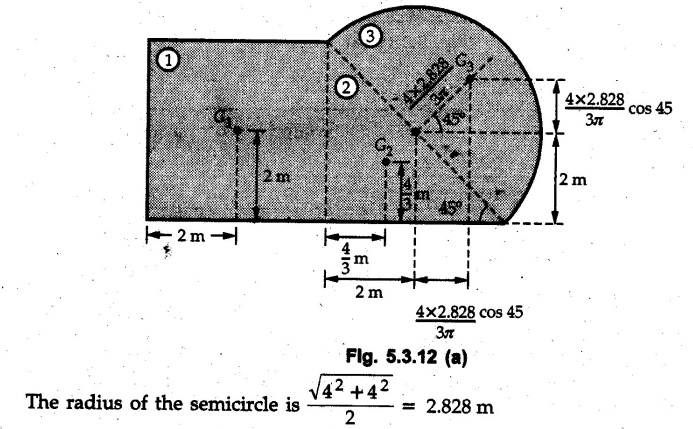
The calculations are tabulated as follows :

Example 5.3.13
Determine location of centroid of shaded portion of lamina with respect to origin O. Refer Fig. 5.3.13.
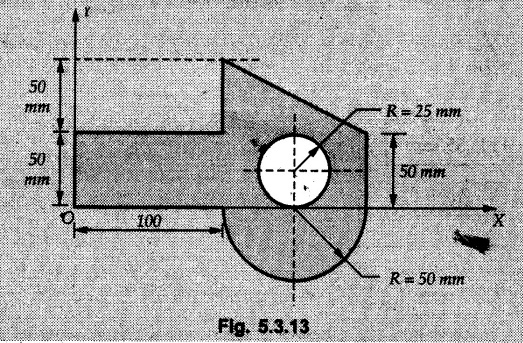
Solution:
The shaded area can be obtained by subtracting area of circle (3) from total area of rectangle ADEH, triangle BCD and semicircle EFG as shown in Fig. 5.3.13 (a).
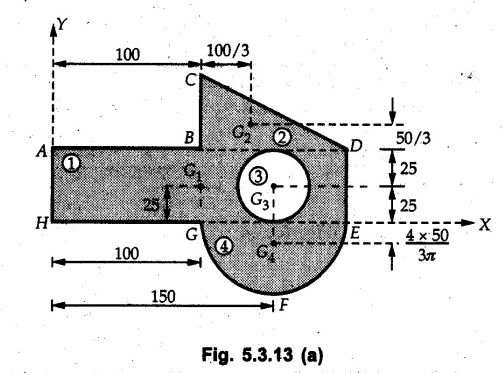
The calculations are tabulated as follows:

Example 5.3.14
A metal piece of uniform thickness is placed on horizontal surface as shown in Fig. 5.3.14. Find distance ‘d’ so that the piece will just be prevented from tipping. Diameter of the hole is 50 mm.
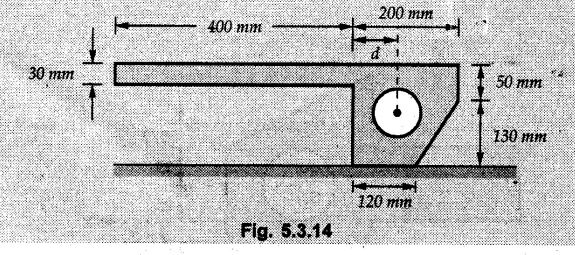
Solution :
Tipping will take place about O.
Divide the area as shown in Fig. 5.3.14 (a). The triangle (4) and circle (3) have to be removed from the total area of rectangles (1) and (2). Take moment of area about O, treating moment of area to the left of O as positive and to the right as negative.

Example 5.3.15
A thin lamina of uniform thickness is as shown in Fig. 5.3.15. If it is suspended from the point A by a wire, what angle will line AB make with vertical ?
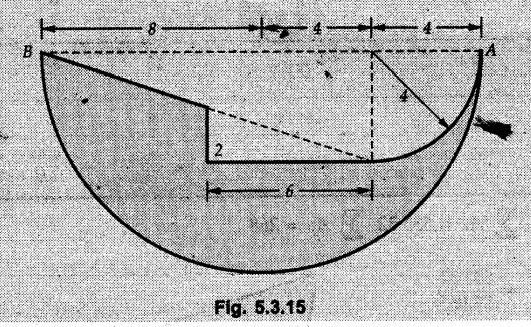
Solution:
As the given lamina is suspended from point A, choose A as the origin and find co-ordinates of centroid G. For convenience we take X-axis towards left and Y-axis downward. When the lamina is suspended from point A, the line AG rotates and X 1 becomes vertical. AG will rotate by angle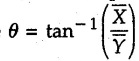 which is the angle made by AG in anticlockwise sense with vertical as shown Fig. 5.3.15 (b). AB will also rotate through the same angle from its horizontal position. Hence angle made by AB with vertical will be 90 – θ.
which is the angle made by AG in anticlockwise sense with vertical as shown Fig. 5.3.15 (b). AB will also rotate through the same angle from its horizontal position. Hence angle made by AB with vertical will be 90 – θ.
We divide the given area into 4 components as shown in Fig. 5.3.15 (a). We subtract triangle (2), rectangle (3) and quarter circle (4) from the semicircle (1). The locations of centroids of the basic shapes are shown as G1, G2, G3, and G4.

The calculations are tabulated as follows:

⸫ Angle made by AB with vertical = 90 – 63.42 = 26.58°
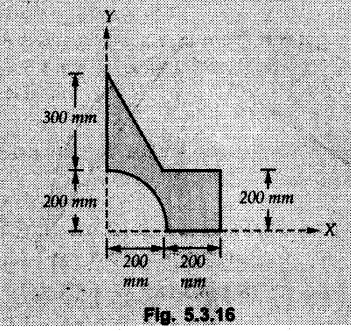
Example 5.3.16
Determine, the co-ordinates of centroid of the shaded portion shown in Fig. 5.3.16.
Solution:
Divide the area into three components as shown in Fig. 5.3.16 (a). The calculations are tabulated as follows.
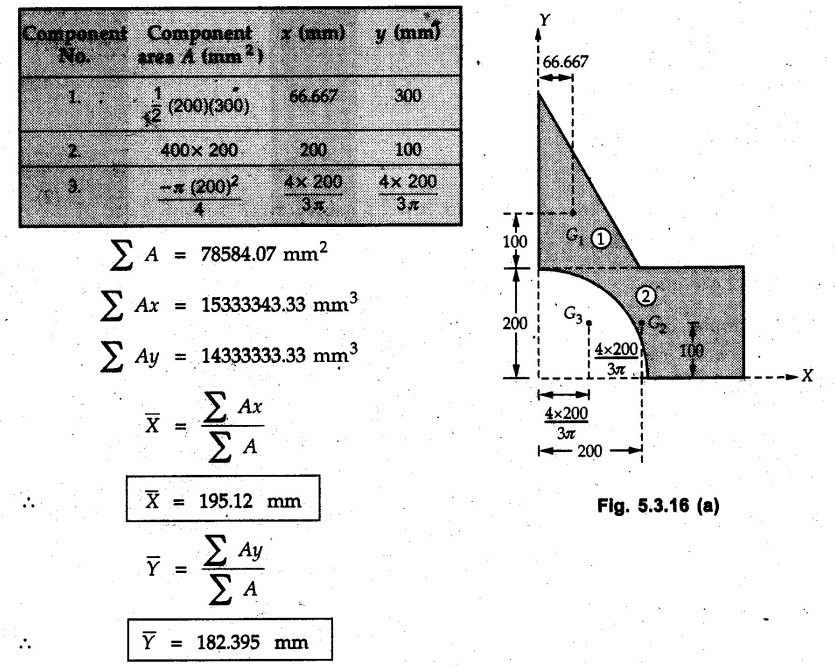
Example 5.3.17
Locate the centroid of shaded portion of a lamina if AB = 90 mm is diameter of semicircle. Refer Fig. 5.3.17.
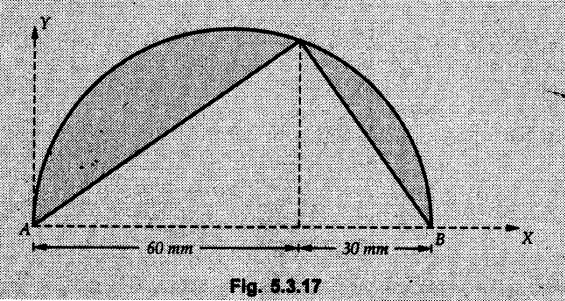
Solution:
The shaded area can be obtained by subtracting the two right angled triangles from the semicircle.
From figure,
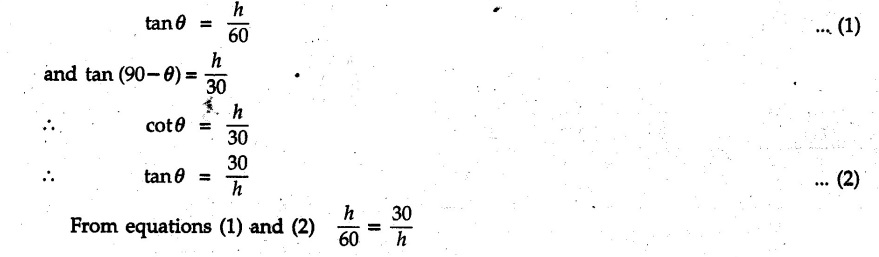
⸫ h = 42.426 mm
The centroids of the three components are as shown in Fig. 5.3.17 (a).

The calculations are tabulated as follows.
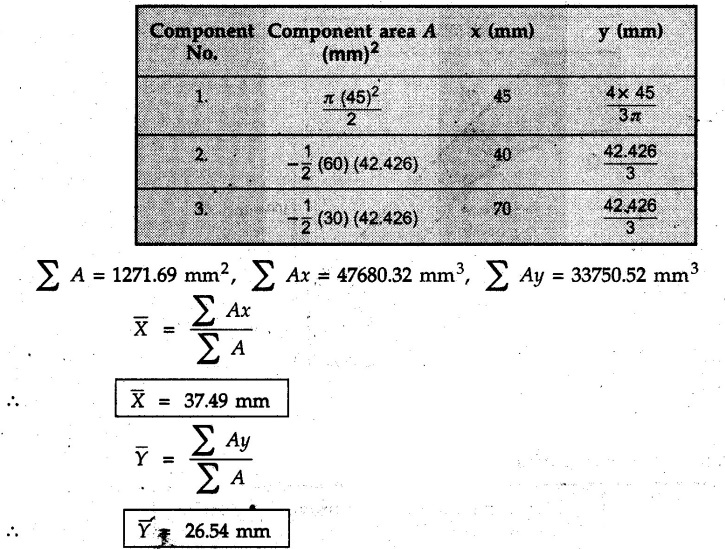
Example 5.3.18
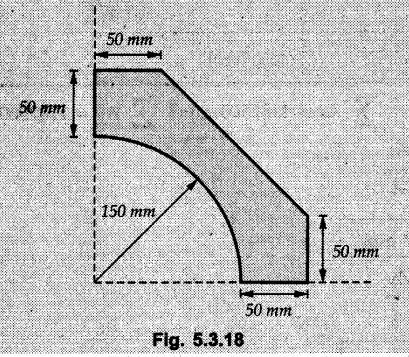
Locate the centroid of the shaded lamina as shown in Fig. 5.3.18.
Solution:
The shaded area can be obtained by subtracting the area of quarter circle and triangle from the area of square. The centroids of components are as shown in Fig. 5.3.18 (a).
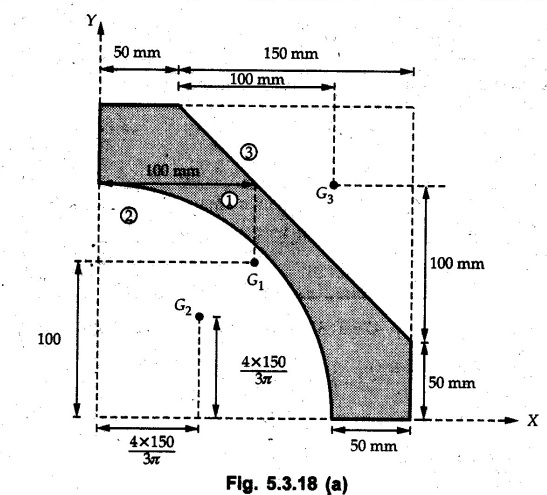
The calculations are tabulated as follows.

Example 5.3.19
Locate the centre of gravity of the area shown in the following Fig. 5.3.19 with respect to the x and y axis. The dimensions shown are in cm.

Solution:
Divide the area as shown in Fig. 5.3.19 (a) and mark the centre of gravity of each standard shape.
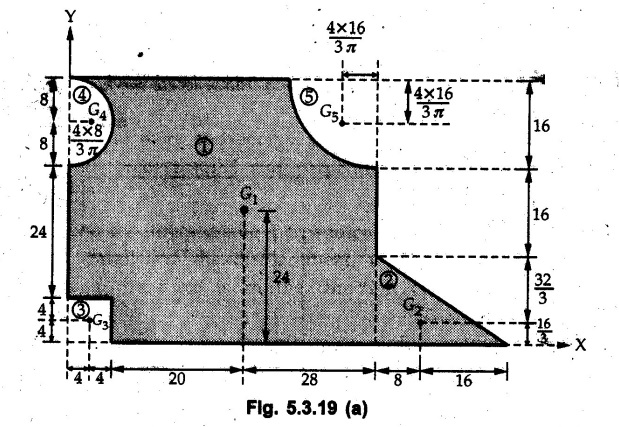
The calculations are tabulated as follows:

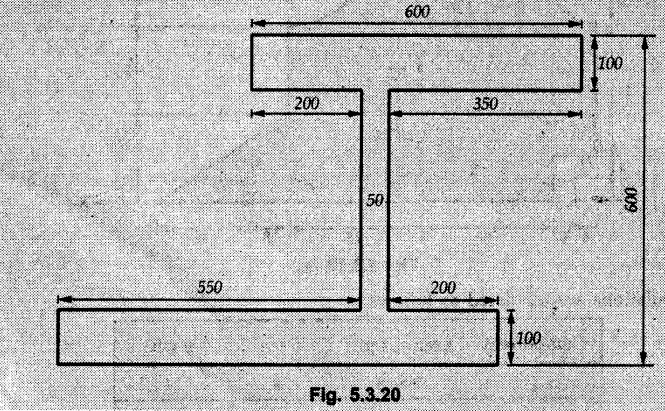
Example 5.3.20
For the section shown in Fig. 5.3,20 below, locate the horizontal and vertical centroidal axes.
 Solution:
Solution:
Take origin as shown in Fig. 5.3.20 (a) and divide the given area into three rectangles.

The calculations are tabulated as follows:

The vertical line passing through![]() = 515.625 is the vertical centroidal axis.
= 515.625 is the vertical centroidal axis.
The horizontal line passing through![]() = 268.75 is the horizontal centroidal axis.
= 268.75 is the horizontal centroidal axis.
Example 5.3.21
Locate the centroid of the plane lamina as shown in Fig. 5.3.21.
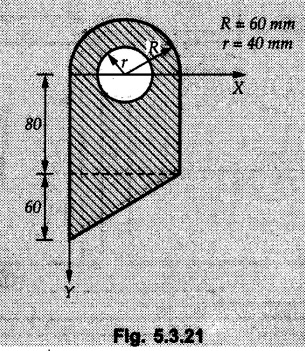
Solution:
The calculated are tabulated as follows:

Example 5.3.22
Locate centroid with respect to O. Refer Fig. 5.3.22.
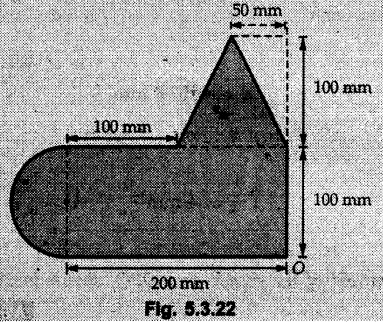
Solution:
The given lamina can be divided into 3 parts a rectangle, an equilateral triangle and a semicircle with centroids as shown in Fig. 5.3.22 (a). The calculations are tabulated as follows:

Example 5.3.23
Find the centroid of the shaded area OPQ, shown in Fig. 5.3.23. The curve OQ is parabolic.
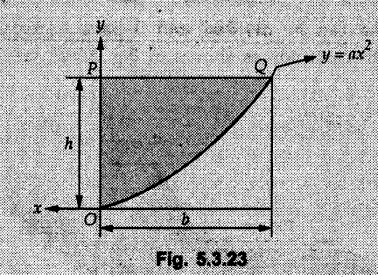
Solution :
At x = b, y = h

Consider the differential element to be a horizontal strip of length x and width dy as shown in Fig. 5.3.23(a).
Area of differential element is
dA = x dy
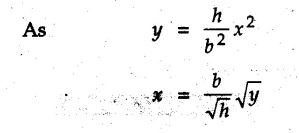
Only positive root is taken as the given area is entirely in first quadrant.

Taking moment of the area about y-axis,
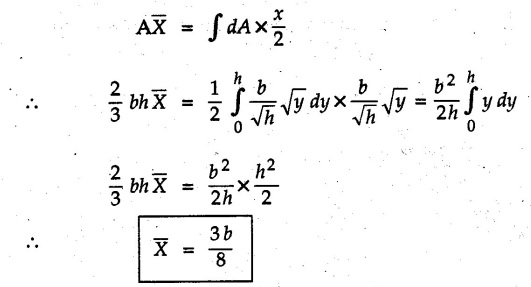
Taking moment of the area about x-axis,

Example 5.3.24
Determine the coordinates of the centroid of the shaded area Fig. 5.3.24.
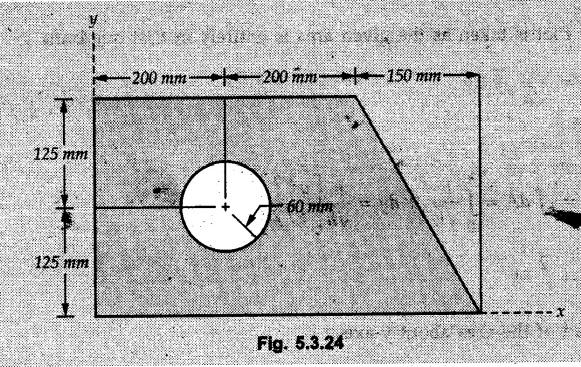
Solution :
Divide the given area into a rectangle, a triangle and a circle as shown in Fig. 5.3.24 (a).
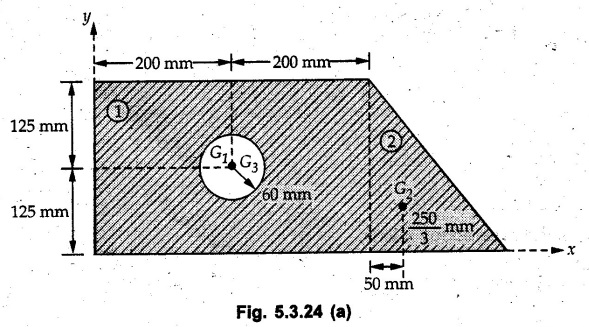
The calculations are tabulated as follows:

Example 5.3.25
Determine the centroid of the area shown in Fig. 5.3.25.
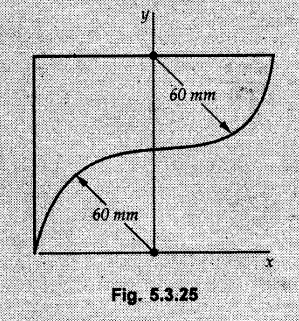
Solution:
The given area can be obtained by adding areas of rectangle and quarter circle and then subtracting area of quarter circle at the bottom as shown in Fig. 5:3.25 (a).
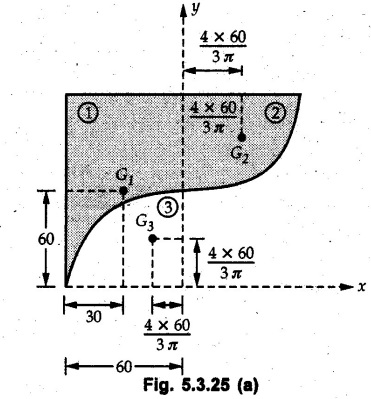
The calculations are tabulated as follows:

Example 5.3.26
Find the centroid of the shaded area shown in Fig. 5.3.26 about X and Y axes.
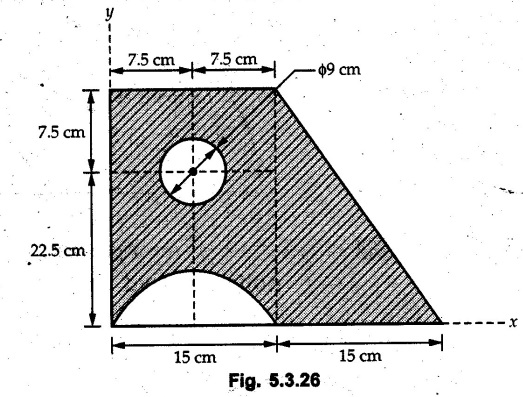
Solution :

Example 5.3.27
From a semicircular lamina of radius r, a circular lamina of radius (r/2) removed as shown in Fig. 5.3.27. Find the position of centre of gravity of the remainder.
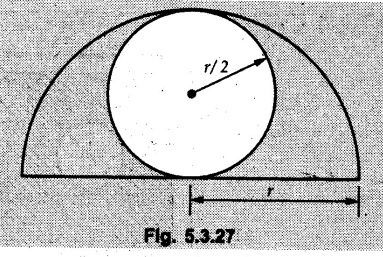
Solution :
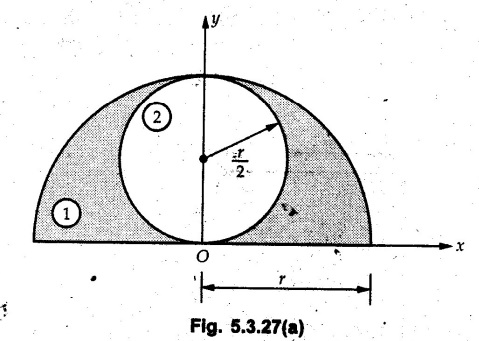
Given Fig. 5.3.27(a) is symmetric about y-axis, hence




Leave a comment